Notes from the most recent London Machine Learning Meetup. There were three talks, the last two were especially interesting to me… so here we go!
Recurrent Models for Machine Perception
- Speaker: Ronnie Clark (Imperial College)
- by “recurrent”, he means more generally iterative algorithms, including optimisers and filters as well as RNNs
- first, RNNs for visual-inertial odometry
- estimating position from 2 data streams - RGB camera and IMU sensors
- rates of data streams are very different (order of magnitude) => multi-rate LSTM
- run 1 for 10 steps, other just 1 step, concat the outputs and run through a “core” LSTM
- next up, SLAM - estimating both camera pose and depth map
- traditional methods alternately estimate pose & depth, and need lots of images
- use ML to predict depth from 1 or 2 images (!)
- can we learn representations to help the optimisation?
- of course we can!
- autoencoder for depth maps to learn compressed code (note that depth maps exhibit sparse structure)
- condition the autoencoder on RGB image
- then can combine to get a model that predicts depth map directly from RGB
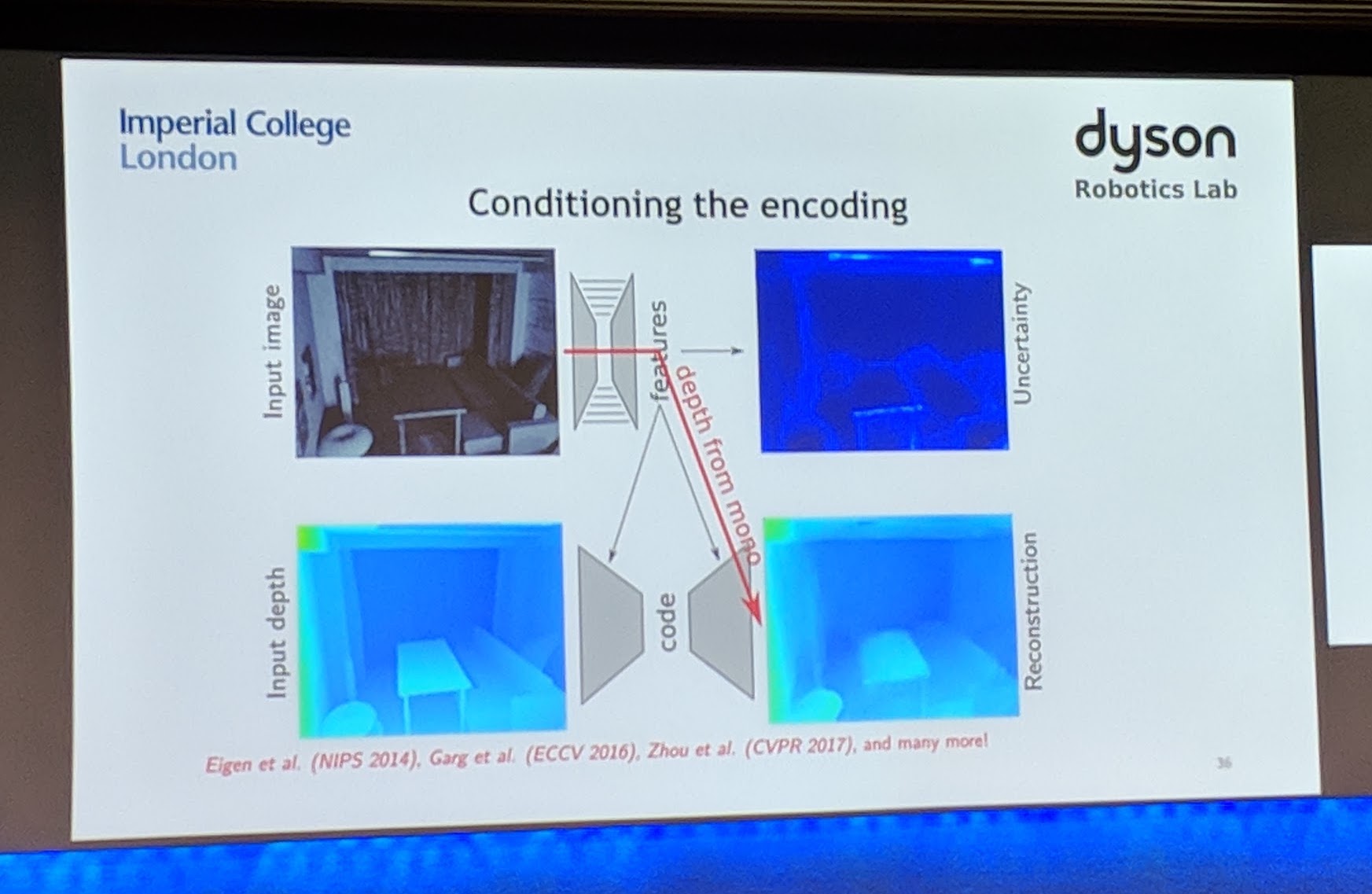
- enables us to optimise depth and pose jointly
- upping the ante - let’s just learn how to optimise the whole damn thing by throwing an LSTM at it
- LSTM learns to compute the update step
- able to converge much faster
- results are not as good but can actually be much sharper (no compression into code, LSTM can theoretically act on any pixel)
Deep Frank-Wolfe
- Speaker: Leo Berrada (Oxford University)
- training DNNs sucks - nonconvex, non-smooth, many terms, high dimensionality
- SGD works well but is sensitive to learning rate
- various designs for learning rate schedule
- no consensus on what’s best, expensive to cross-validate
- adaptive gradient methods are simpler to use
- but tend to have poor generalisation performance (Wilson et al. 2017)
- we want ease of use and good generalisation
- consider… SVM training - convex, smooth in dual, hyperparam-free and efficient optimisation
- some maths -> proximal equivalence for SGD update step
- minimisation problem with a constraint that we stay close (proximal) to the current weights
- uses a full linearisation of the loss function
- but if we instead use a loss-preserving linearisation, we get a linear SVM

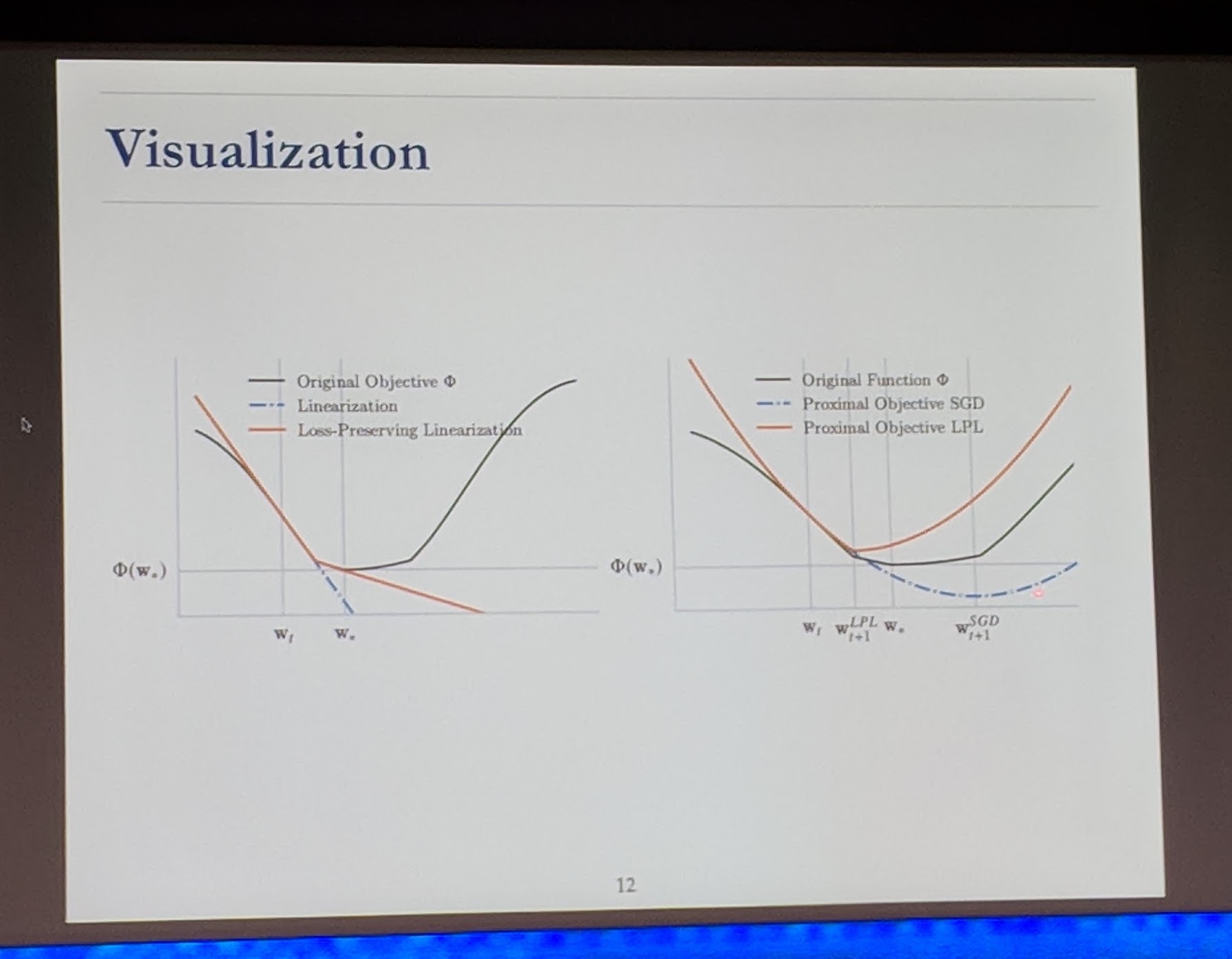
- solve the proximal problem with Frank-Wolfe, as for SVMs
- get step size in closed form
- same direction as SGD => same computation cost
- make this faster by running just 1 iteration of Frank-Wolfe per proximal problem
- we’re approximating anyway, just like SGD
- they claim it’s just 10% more expensive than SGD
- can also adapt this to use momentum
- experiments for legit models on CIFAR and SNLI
- DFW performs comparably to the custom-designed, dataset- and architecture-specific learning rate schedules proposed by the original authors of the models (?!)
- why so good?
- empirically, large initial steps
- intuitively, by preserving more info about the loss function, we can be more robust to step size
- some audience questions
- they haven’t really thought about how this works together with batch size. There is some audience incredulity at this, given academic and practical interest in batch sizes.
- no theoretical guarantees of convergence, just an empirical result
- the speaker made a bunch of excuses about how momentum screws up the theory, but I’m still wondering, what about if you just ignore momentum, what screws it up then?
- code is not yet up but they promised it here
Verifying Neural Networks
- Speaker: Rudy Bunel (Oxford University)
- this wasn’t the name of the talk but I didn’t write it down and it’s not posted on the meetup page, sorry!!
- setup: given a trained NN, prove that a property holds over the output, for a given input region
- example applications:
- robustness to adversarial examples
- anytime you care about safety
- existing methods are mainly using a validation set to test against adversarial attacks
- “Testing can be a very effective way to show the presence of bugs, but it is hopelessly inadequate for showing their absence” – Dijkstra
- we want to make definite statements in research (wow, what a notion)
- canonical problem: any property taking the form of a boolean formula over linear inequalities can be reduced to a lower bound property (possibly over a different network)
- so proving the property holds just requires a global minimum over the outputs
- if the global min is above the bound, we’re okay, otherwise not
- unfortunately getting the global min is…… hard
- solution #1: mixed integer programming
- NP-hard but just use commercial solvers, it’ll be fine
- solution #2: branch and bound
- bound: estimate the worst-case overapproximation of input region at each layer of the network
- branch: split into smaller regions to improve approximation if needed
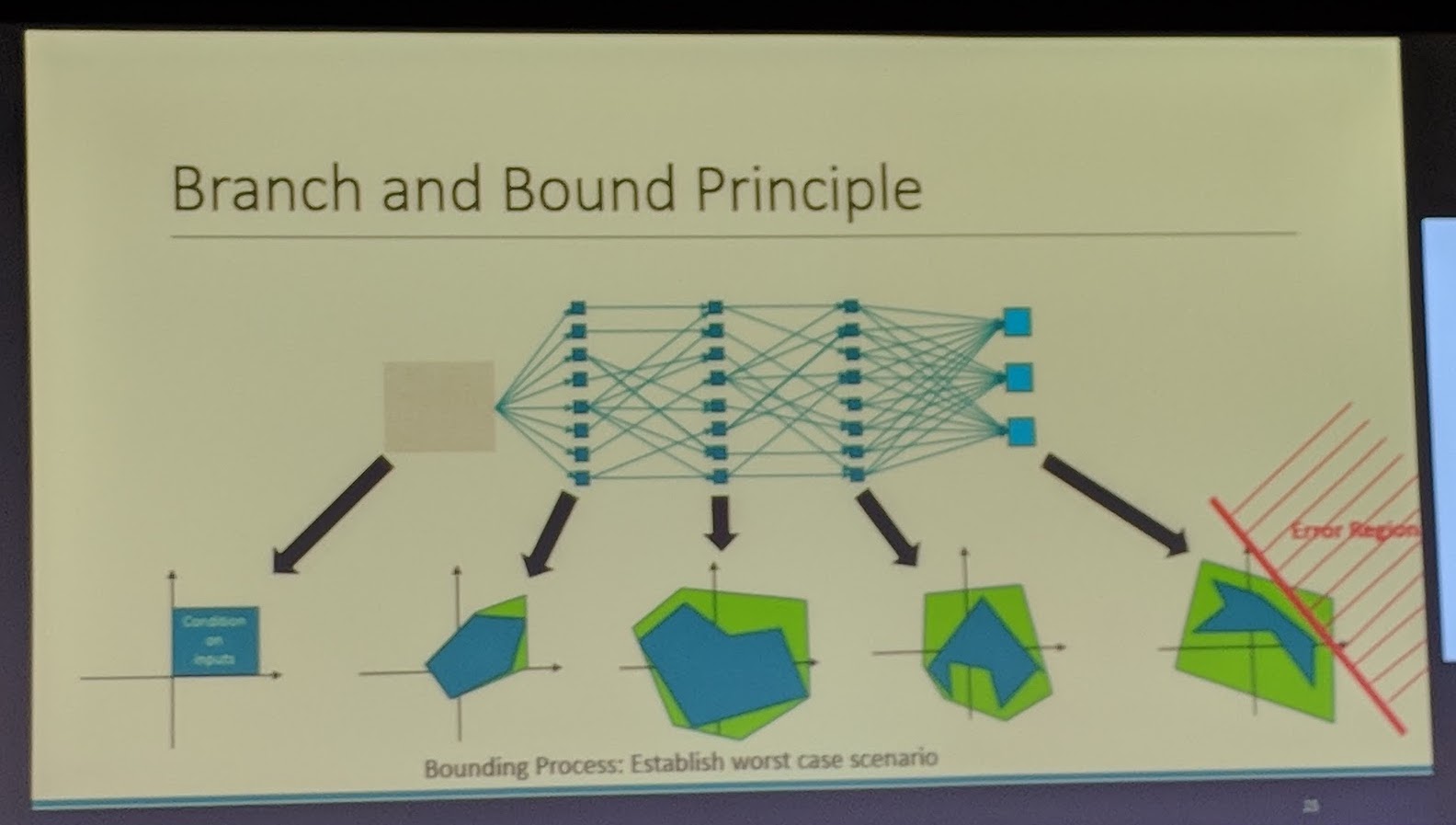
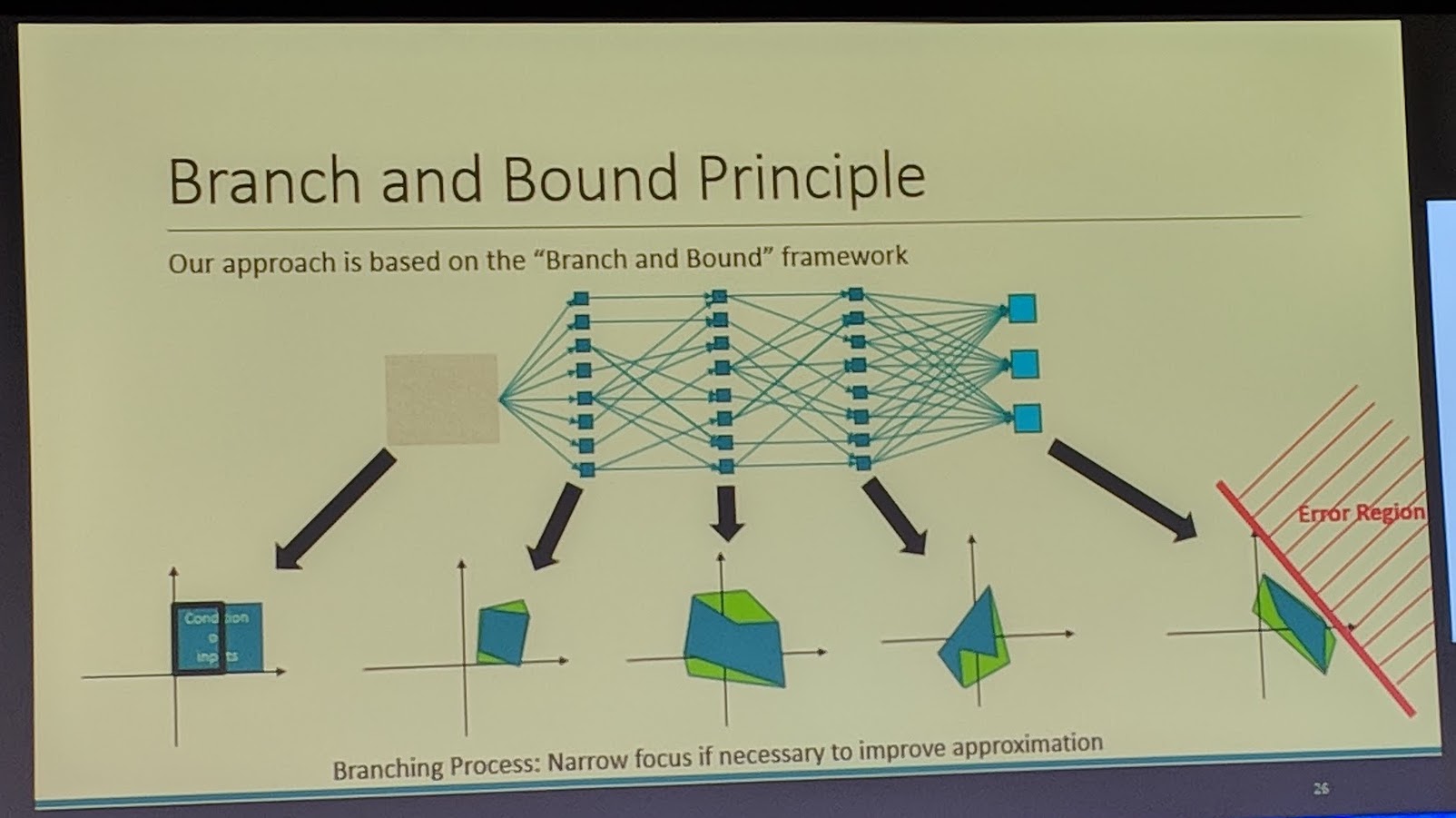
- this constitutes a general framework for some other DNN verification techniques in the literature
- Ruediger Ehlers 2017 - networks with piecewise linear activations
- Wong & Kolter, ICML 2018 - deep ReLU-based classifiers
- actually does okay in practice too
- tested on ACAS dataset, for systems which are deployed in aircraft and must be safe
- can also use these methods in the training loop to improve robustness to adversaries etc.
- one of the biggest challenges is how to specify your desired properties in the right language
- indeed, my takeaway from this is that it’s incredibly interesting work and potentially of great utility, but applying it to your domain and your models is likely to be highly non-trivial, at least for now